¿Por qué es tan famoso el número PI?

El número Pi también llamado proporción áurea ha existido siempre en el universo físico y se puede explicar de forma matemática. Pero el hombre a lo largo de la historia lo ha descubierto y re descubierto alguna vez. Como muchas otros temas científicos y matemáticos el numero Pi era conocido en la antigua Grecia. Después estos conocimientos fueron olvidados para ser re descubierto más tarde en la historia. Es por esto también que este número recibe varios nombres.

¿Cuáles fueron sus primeros hallazgos? .

El primer hallazgo fue hecho por Pitágoras ,que nació en la isla de Samos (Grecia), en el 570 a. C. y murió en Metaponto en el 469 a. C., hijo de Mnesarco. Fue discípulo de Tales y de Fenecidas de Siria, estudió en la escuela de Mileto. Viajó por Oriente Medio (Egipto y Babilonia). Sufrió el exilio para escapar de la tiranía del dictador Samio Polícrates, por lo que vagabundeó hasta establecerse en el 531 a. C. en las colonias italianas de Grecia donde fundó su famosa escuela pitagórica en Crotona al sur de Italia.

Dado que en la práctica de medir la longitud de un segmento de recta solo puede producir como resultado un número fraccionario, en un inicio, los griegos identificaron los números con las longitudes de los segmentos de recta Al identificar del modo mencionado, surgió la necesidad de considerar una clase de números más amplia que la de los números fraccionarios. Por eso mismo, se atribuye a Pitágoras y su escuela el descubrimiento de la existencia de segmentos de recta inconmensurables con respecto a un segmento que se toma como unidad en un sistema de medición. Pues, existen segmentos de recta cuya longitud medida en este sistema no es un número fraccionario.

Por ejemplo, en un cuadrado, la diagonal de este es inconmensurable con respecto a sus lados. Este hecho ocasionó una convulsión en el mundo científico antiguo. Provocó una ruptura entre la geometría y la aritmética de aquella época, ya que esta última, por entonces, se sustentaba en la teoría de la proporcionalidad, la cual solo se aplica a magnitudes conmensurables.

¿Qué clase de número es raíz cuadrada de 5?

La raíz cuadrada de 5 es el número real positivo que, cuando es multiplicado por sí mismo, da el número primo 5. Este número es notable en parte porque aparece en la fórmula para el número áureo. La raíz cuadrada de 5 es un número irracional algebraico

4- La longitud de una circunferencia es igual a pi por el diámetro.

La longitud de una circunferencia depende de dos valores, uno de ellos se mantiene invariable, el valor de PI  geometría y el otro valor el del radio. Cuanto mayor sea el valor del radio, mayor será la longitud de la circunferencia y el otro factor que aparece en todo los cálculos de longitudes de circunferencias y se mantiene siempre con el mismo valor sea grande como pequeña la figura es geometría La longitud de la circunferencia depende del tamaño del radio. El factor geometría se mantiene en el cálculo de las longitudes de todas las circunferencias.

ELE Es necesario que aprendas los elementos de toda circunferencia:

1) centro. El punto del que equidistan todos los puntos de la circunferencia.

2) radio. Segmento que une el centro con cualquier punto de la circunferencia.

3) cuerda: Segmento que une dos puntos cualesquiera de la circunferencia sin que pase por el centro: MENTOS DE UNA CIRCUNFERENCIA

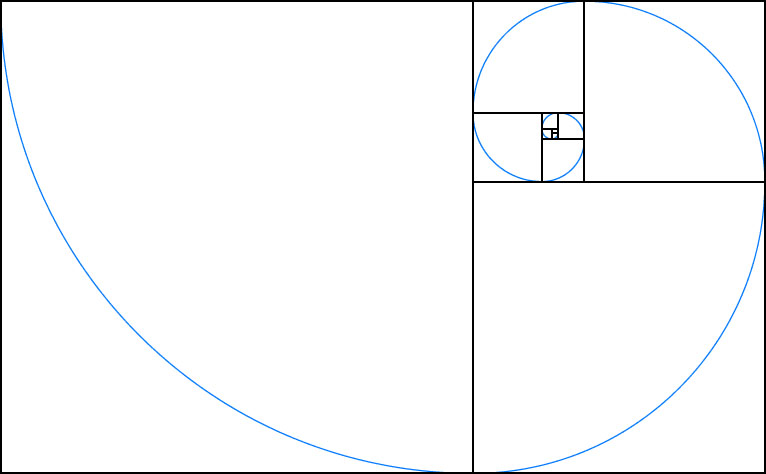
¿Qué es la divina proporción?

La divina proporción es la proporción perfecta entre dos lados de un rectángulo. Ha sido importante a lo largo de la historia de artes plásticas y en la arquitectura.

¿Qué es un número irracional?

El concepto proviene de la Escuela Pitagórica, donde se descubrió la existencia de este tipo de números, que no eran enteros ni racionales, como fracciones. Primero, se los llamo "números incomensurables"

¿Qué es un número irracional?
Son números que poseen infinitas cifras decimales (no periódicas) q no pueden ser expresdos como fracciones.

¿Cómo se descubrieron?
Lo más probable es que estos números fueron descubiertos al tratar de resolver la longitud de un cuadrado (teorema de pitágoras), y el resultado fue

O también, resolver la raíz cuadrada de dos, el mejor ejemplo para los números irracionales. Su respuesta posee infinitas cifras decimales y como no se pudo fraccionar, se le llamó iraccional, ya que no se puede escribirlo como una ración o fracción.


¿Cómo se distinguen los números irracionales de los racionales?
Para distinguirlos debemos tomar en cuenta que los números racionales se pueden fraccionar.Por ejemplo, 18/5 es igual a 3,6 y es un número raccional a difrencia de  √2, por que el resultado de esta misma tiene infinitas cifras decimales, esto hace que su fraccionamiento resulte imposible.

De esta manera podemos definir a los números irracionales como un decimal infinito no periódico, es decir que cualquier representación de un número irracional, solo es una aproximación en números racionales.

  ¿Cómo se realiza la notación? Se hace con las letras mayúsculas : 

Se la utiliza de esta manera para diferenciarla de los números imaginarios, cuya representación es la i minúscula. 

Existen algunos casos especiales de números irracionales que tienen su propia notación, como por ejemplo : 

Pi, o como se lo conoce mejor con su símbolo π, es el más conocido y el más utilizado. Su valor es el cociente entre la longitud o perímetro de la circunferencia y la longitud de su diámetro. Con él se calcularon millones de cifras decimales pero todavía  no se encuentra el patrón exacto, el número de aproximación es el siguiente : 

¿Cuáles son sus propiedades?

Sus propiedades son : 

La propiedad conmutativa: El orden de los factores no altera el resultado. π×ϕ=ϕ×π

La propiedad asociativa: La agrupación de los números da como resultado el mismo número, sin importar la agrupación,siendo (ϕ+π)+e=ϕ+ (π+e); y de la misma manera con la multiplicación, (ϕ×π) ×e=ϕ× (π×e).

Elemento opuesto:  Cada número tiene su negativo que lo anula, π-π=0 y de la misma forma un inverso multiplicativo que da como resultado 1, es decir ϕ×1/ϕ=1.

¿Cómo se clasifican?

Se clasifican en estos tres grupos : 

Elemento opuesto:  Cada número tiene su negativo que lo anula, π-π=0 y de la misma forma un inverso multiplicativo que da como resultado 1, es decir ϕ×1/ϕ=1.

Número algebraico : números irracionales que surgen de resolver alguna ecuación algebraica y se escribe con un número finito de radicales libres o anidados.

Número trascendente.- número irracional que no puede ser representado a través de un número finito de radicales libres o anidados. Provienen de las funciones trascendentes, utilizadas en por ejemplo, la trigonometría. También puede surgir de escribir números decimales al azar y sin un patrón determinado.